Pratt Parsing

I recently stumbled into a Pratt parsing based parser at work. A helpful collegue send me this article: Simple but Powerful Pratt Parsing, which does a great job at explaining things, but it still had me staring at the minimal implementation for a long time before I got it (with said collegues help, thank you Rasmus). So this post is for you if you don't have Rasmus handy. If you just want a general introduction to Pratt parsers read that article instead and then come back if you get stuck.

I think there where two things that made it hard for me to parse the code, other than it just being rather complex. First we have two recursive methods calling each other. This is a bit hidden in (link) because a loop is used in the outer method rather than an explicit, named, inner recursive function, and then the loop breaks and you have to find the return value outside the loop. Secondly a global state is hidden inside the lexer making it kind of hard to track the remaining tokens.

So here is my F# version that adresses that. It uses two named recursive functions and there is no hidden state or other side effects (the functions return a tuple : (expression, remaining tokens)).

let rec ParseFromLiteral tokens minBindingPower =
    let rec ParseFromOperator lhs tokens =
        match tokens with
            | [] -> lhs, []
            | Operator op::_ when op.LeftBindingPower < minBindingPower ->
                lhs, tokens
            | Operator op::rest ->
                let rhs, rhsRest = ParseFromLiteral rest op.RightBindingPower
                ParseFromOperator (Expression(op, lhs, rhs))  rhsRest
            | _ -> failwith $"Expected operator in {tokens}."
    match tokens with
        | [Token.Literal c] -> Literal c, []
        | Token.Literal c::tail -> ParseFromOperator (Literal c) tail
        | _ -> failwith "Expected literal in {tokens}."

A third thing I struggled with in the article, but also reading Bob Nystroms excellent article was the focus on prefix vs. infix. Basically it seemed to me that it if ex. I only have number literals and the Add and substract operators in my language, it does not really matter that add and subtract are infix operators. I can apply them as soon as i have parsed the next literal. with a single level of recursion.

let parse expr tokens =
   let lhs = tokens.head
   let op = (List.skip 1 tokens).Head
   (op, lhs, parse (List.skip 2 tokens))

This only breaks when I start to have different binding power between operators, once we introduce multiply or divide operators I cannot apply my operators immediately; I have to discover if the next token is followed by an operator of greater power, and then apply that first. So infix is really just a pre-requisite, it’s operators with unequal bindingpower that really causes the headache.

So lets look at the first thing that breaks the simple recursive parser above: A*B+C would be parsed as (* A (+ (B C)) but should of course be (+ (C (* A B)). Lets track how the Pratt parser gets it right:

1. Parse (* A B….
2. Recurse down to finish the expression Here there are two ways of doing it: 2a. We can recursively form the next expression inside the outer expression. Equivalent to the simple recursive decent parser above. We would get (* A (? B ?)) Or: 2b. Discover that the next operator + is weaker binding than * and instead finish the expression by using what has been parsed so far as the inner left hand side of a new outer expression (formed by the outmost parser) (? (* A B) ?).

More generally it helped me to think in terms of building the tree representation of the s-expression. In the simple recursive decent parser my only choice is to build a very unbalanced tree, every operator parsed grows the right hand side of the tree one level deeper. The pratt parser gains the ability to promote a new operator to the top of the tree, appointing what we have seen so far to the lhs of the new root and continuing construction of the rhs.

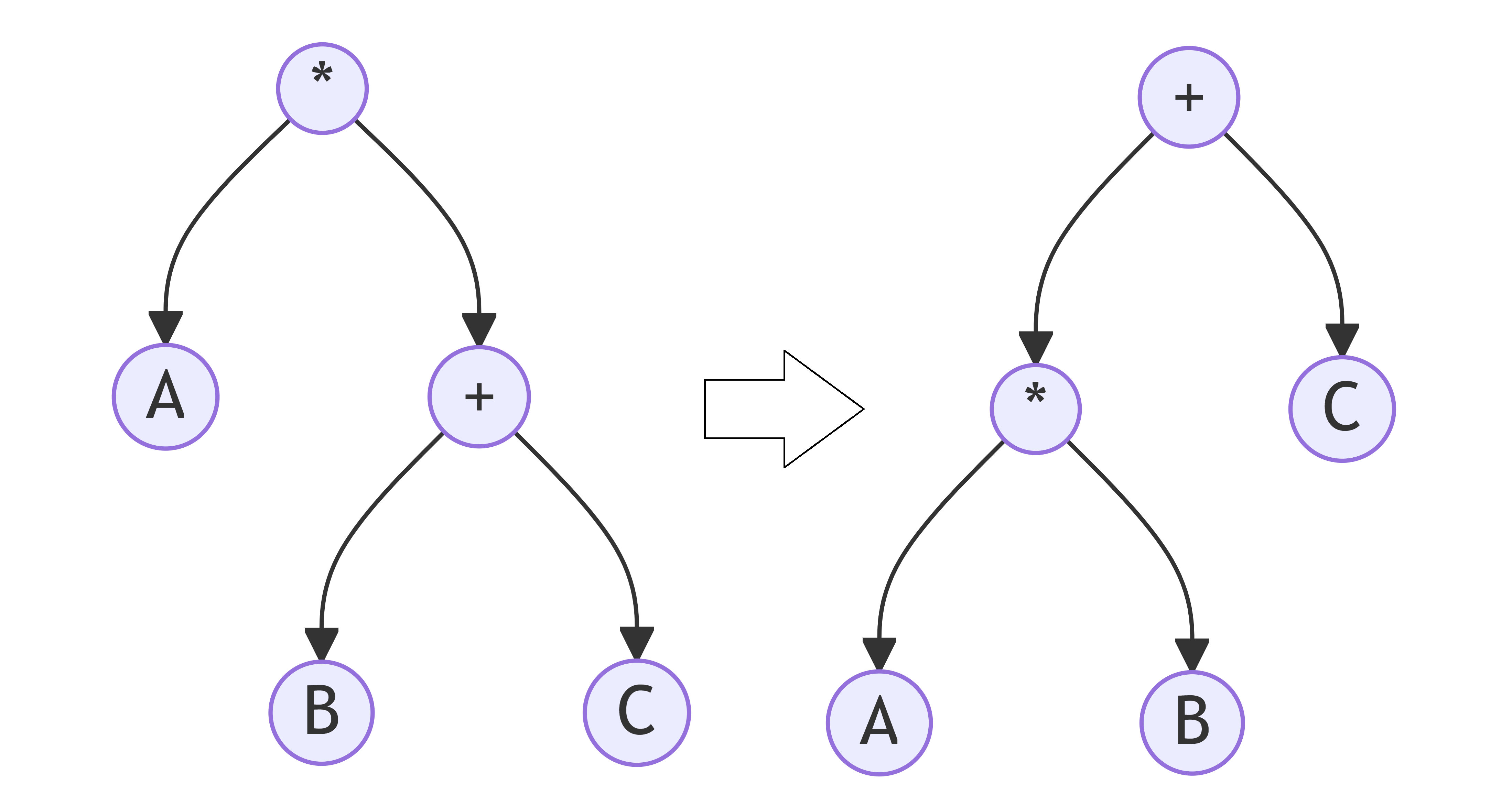
In the Pratt parser we can also keep recursing, i.e. growing down the right hand side, but once we pop back out is the promotion moment, at that point a finished expression is formed and the next operator is promoted to apply with that expression on the lhs, rather than inside its rhs as would normally be the case. It becomes a parent rather than a child in the tree view.

let rhs, rhsRest = ParseFromLiteral rest op.RightBindingPower
//   ▲ parse rhs -> form lhs ▼                
ParseFromOperator (Expression(op, lhs, rhs))  rhsRest

Now this decision is made only when binding powers are at play, which means when parsing operators. I found that this split was the cleanest distinction i could make between the two recursive methods. Hence I called my methods ParseFromOperator and ParseFromLiteral.

I can’t recall seeing other algorithms that combine two recursive methods like this, with the inner recursion calling both methods. It certainly is a challenge to wrap your head around and really a work of art. If you know of others please do let me know.

My full code including the lexer etc. is included here:

type Operator =
    | Multiply
    | Add
    with
        member this.BindingPower =
            match this with
                | Multiply -> (3,4)
                | Add -> (1,2)
        member this.LeftBindingPower =
           fst this.BindingPower
        member this.RightBindingPower =
           snd (this.BindingPower)
        override this.ToString() =
            match this with
                | Multiply -> "*"
                | Add -> "+"

type Token = Literal of char | Operator of Operator

let lexer :seq<char> -> Token list =
    Seq.filter ((<>) ' ')  >>
    Seq.map (function
             | '*' -> Operator(Multiply)
             | '+' -> Operator(Add)
             | c -> Literal(c)) >> Seq.toList

type Expression =
    | Literal of char | Expression of Operator * Expression * Expression
    override this.ToString() =
        match this with
            | Literal(c) -> $"{c}"
            | Expression(op, left, right) -> $"({op} {left}  {right})"

let rec ParseFromLiteral tokens minBindingPower =
    let rec ParseFromOperator lhs tokens =
        match tokens with
            | [] -> lhs, []
            | Operator op::_ when op.LeftBindingPower < minBindingPower ->
                lhs, tokens
            | Operator op::rest ->
                let rhs, rhsRest = ParseFromLiteral rest op.RightBindingPower
                ParseFromOperator (Expression(op, lhs, rhs))  rhsRest
            | _ -> failwith $"Expected operator in {tokens}."
    match tokens with
        | [Token.Literal c] -> Literal c, []
        | Token.Literal c::tail -> ParseFromOperator (Literal c) tail
        | _ -> failwith "Expected literal in {tokens}."                

let ParseString input =
    (fst (ParseFromLiteral (lexer input) 0)).ToString()

printfn $"""ParseString "1 * 2 + 3" -> {ParseString "1 * 2 + 3"}"""
printfn $"""ParseString "1 + 2 * 3" -> {ParseString "1 + 2 * 3"}"""
printfn $"""ParseString "a + b * c * d + e" -> {ParseString "a + b * c * d + e"}"""